二叉树的定义:
是一颗空树或者具有以下性质
1.结点最多只有两个孩子,且有左右之分。不能交换左右孩子
2.结点点的左子树和右子树也是二叉树。
例图
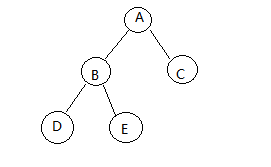
二叉树的基本形态:
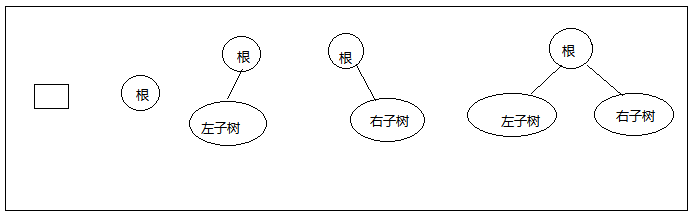
二叉树中的术语:
1).结点度:节点所拥有的字数的个数成为该节点的度,在二叉树中度的取值只能是0,1,2.
2).叶节点:度为0的节点成为叶结点或终端结点。
3).左孩子、右孩子、双亲:树中一个结点的子树的根结点称为这个结点的孩子。这个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。
4).路径、路径长度:如果一棵树的一串结点n1,n2,…,nk有如下关系:结点ni是ni+1的父结点(1≤i<k),就把n1,n2,…,nk称为一条由n1至nk的路径。这条路径的长度是k-1。
5).结点的层数:规定树的根结点的层数为1,其余结点的层数等于它的双亲结点的层数加1。
6).树的深度:树中所有结点的最大层数称为树的深度。
7).满二叉树。 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都在同一层上,这样的一棵二叉树称作满二叉树。
8).完全二叉树。一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为 i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。完全二叉树的特点是:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左 部。
二叉树的性质:
1).非空二叉树叶子结点数等于度为2的结点数加1,即N0=N2+1.(其中N0和N2分别是叶结点和度为2结点的个数)。
2).非空二叉树第K层上最多有 2^(k - 1)个结点(K>= 1).
3).高度为H的节点,最多有2^H - 1个节点(H >= 1).
二叉树的基本操作:
/*以下为二叉树的常用操作(如有错误之处还望之处)
采用二叉链表的存储结构*/
1 typedef struct BiTNode //二叉树的节点2 {3 DataType m_Value;4 BiTNode *m_pLeft;5 BiTNode *m_pRight;6 }BiTNode; //创建二叉树(先序)
1 //创建二叉树(先序) 2 void createBiTree(BiTNode * &pCurrent) 3 { 4 cout << "先序输入节点:"; 5 DataType value; 6 cin >> value ; 7 if(value == '#') 8 pCurrent = NULL; 9 else10 {11 pCurrent = (BiTNode *)malloc(sizeof(BiTNode));12 pCurrent->m_Value = value;13 createBiTree(pCurrent->m_pLeft);14 createBiTree(pCurrent->m_pRight);15 }16 } //递归实现前序遍历二叉树
1 void preOrderVisitUseRecur(const BiTNode * pCurrent)2 {3 if(pCurrent)4 {5 cout << pCurrent->m_Value << " ";6 preOrderVisitUseRecur(pCurrent->m_pLeft);7 preOrderVisitUseRecur(pCurrent->m_pRight);8 }9 } //用栈,不用递归实现前序排列
1 void preOrderVisitUseStack(const BiTNode * pCurrent) 2 { 3 stack pNodeStack; 4 const BiTNode *p = pCurrent; 5 while(p||!pNodeStack.empty()) 6 { 7 if(p) //如果该节点不是NULL 8 { 9 cout << pCurrent->m_Value << " "; //访问节点的值10 pNodeStack.push(p); //将节点压栈11 p = p->m_pLeft;12 }13 else14 {15 //如果该节点是NULL16 p = pNodeStack.top(); //获取栈顶元素17 pNodeStack.pop(); //删除栈顶元素18 p = p->m_pRight; //访问右节点19 }20 21 }22 } //递归实现中序遍历
1 void inOrderVisitUseRecur(const BiTNode * pCurrent)2 {3 if(pCurrent)4 {5 inOrderVisitUseRecur(pCurrent->m_pLeft);6 cout << pCurrent->m_Value << " ";7 inOrderVisitUseRecur(pCurrent->m_pRight);8 }9 } //用栈实现中序遍历
1 void inOrderVisitUseStack(const BiTNode * pCurrent) 2 { 3 stack pNodeStack; 4 const BiTNode * p = pCurrent; 5 while(p||!pNodeStack.empty()) 6 { 7 if(p) //如果该节点不是NULL 8 { 9 pNodeStack.push(p); //将节点压栈10 p = p->m_pLeft;11 }12 else13 {14 //如果该节点是NULL15 p = pNodeStack.top(); //获取栈顶元素16 pNodeStack.pop(); //删除栈顶元素17 cout << pCurrent->m_Value << " "; //访问节点的值18 p = p->m_pRight; //访问右节点19 }20 }21 } //递归实现后序遍历
1 void afterOrderVisitUseRecur(const BiTNode * pCurrent)2 {3 if(pCurrent)4 {5 afterOrderVisitUseRecur(pCurrent->m_pLeft);6 afterOrderVisitUseRecur(pCurrent->m_pRight);7 cout << pCurrent->m_Value << " ";8 }9 } //用栈实现后序遍历
1 void afterOrderVisitUseStack(const BiTNode * pCurrent) 2 { 3 stack pNodeStack1; 4 stack pNodeStack2; 5 const BiTNode * p =pCurrent; 6 while(p||!pNodeStack1.empty()) 7 { 8 if(p) //如果该节点不是NULL 9 {10 pNodeStack1.push(p); //将节点压栈11 pNodeStack2.push(p); //将节点压栈12 p = p->m_pRight;13 }14 else15 {16 //如果该节点是NULL17 p = pNodeStack1.top(); //获取栈顶元素18 pNodeStack1.pop(); //删除栈顶元素19 p = p->m_pLeft; //访问左节点20 }21 }22 p = NULL;23 while(!pNodeStack2.empty())24 {25 p = pNodeStack2.top(); //获取栈顶元素26 pNodeStack2.pop(); //删除栈顶元素27 cout << pCurrent->m_Value << " ";28 }29 } //按层次进行遍历(有点小问题)
1 /* 2 void levelOrderVisit(const BiTNode *pCurrent) 3 { 4 deque pNodedeue; 5 const BiTNode * p = NULL; 6 if(pCurrent) 7 { 8 pNodedeue.push_back(pCurrent); //第一次将节点放到队列 9 }10 while(!pNodedeue.empty()||p)11 {12 p = *pNodedeue.begin(); //返回队列首元素,但不删除13 pNodedeue.pop_front(); //删除队首元素14 if(p)15 {16 cout << p->m_Value;17 if(p->m_pLeft)18 pNodedeue.push_back(p); //左孩子不空则进入队列19 if(p->m_pRight)20 pNodedeue.push_back(p); //右孩子不空则进入队列21 }22 }23 }24 */ //计算树的深度
1 int getTreeDepth(const BiTNode * pCurrent) 2 { 3 int leftDepth = 0,rightDepth = 0; 4 if(!pCurrent) 5 { 6 //空的话返回0 7 return 0; 8 } 9 else10 {11 leftDepth = getTreeDepth(pCurrent->m_pLeft); //获得左子树的高度12 rightDepth = getTreeDepth(pCurrent->m_pRight); //获得右子树的高度13 return (leftDepth>rightDepth?leftDepth:rightDepth) + 1;14 }15 } //计算树节点的个数
1 int coutTreeNodeNums(const BiTNode *pCurrent) 2 { 3 int leftNums,rightNums; 4 if(!pCurrent) 5 { 6 return 0; 7 } 8 else 9 {10 leftNums = coutTreeNodeNums(pCurrent->m_pLeft);11 rightNums = coutTreeNodeNums(pCurrent->m_pRight);12 }13 return leftNums + rightNums + 1;14 } //以下是各操作的实例
1 int main() 2 { 3 BiTNode * root = NULL; 4 cout << "start to create a tree:" << endl; 5 createBiTree(root); 6 cout << "visit a tree use 递归先序:" << endl; 7 preOrderVisitUseRecur(root); 8 cout << endl; 9 cout << "visit a tree use 栈先序:" << endl;10 preOrderVisitUseStack(root);11 cout << endl;12 cout << "visit a tree use 递归中序:" << endl;13 inOrderVisitUseRecur(root);14 cout << endl;15 cout << "visit a tree use 栈中序:" << endl;16 inOrderVisitUseStack(root);17 cout << endl;18 cout << "visit a tree use 递归后序:" << endl;19 afterOrderVisitUseRecur(root);20 cout << endl;21 cout << "visit a tree use 栈后序:" << endl;22 afterOrderVisitUseStack(root);23 cout << endl;24 //cout << "层次遍历:" << endl;25 //levelOrderVisit(root);26 cout << "树中节点的个数:" << coutTreeNodeNums(root) << endl;27 cout << "树的深度为:" << getTreeDepth(root) << endl;28 return 0;29 }